1-2. 소수와 합성수

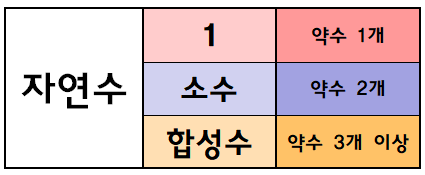
1보다 큰 자연수 중에서

1과 자기 자신만을 약수로 가지는 수를

소수라고 한다.

 

위의 표와 같이 1과 자기 자신을 약수로 가지는 수, 즉

2, 3, 5, 7 이 소수이다.

이때, 소수는 약수가 2개임을 알 수 있다.

tip) 2는 소수중에 유일한 짝수이다.

 

또, 1보다 큰 자연수 중에서

소수가 아닌 수를 합성수라 한다.

 

위의 표에서 소수가 아닌 수, 즉

4, 6, 8, 9, 10은 합성수이다.

이때, 합성수의 약수의 개수는 3개 이상임을 알수 있다.

 

그럼 1은?

1은 약수가 1 뿐이므로 소수도 아니고 합성수도 아니다.

 

자연수는 약수의 개수에 따라 다음과 같이 분류할 수 있다.

 

모든 합성수는 소수들의 곱으로 나타낼 수 있다.

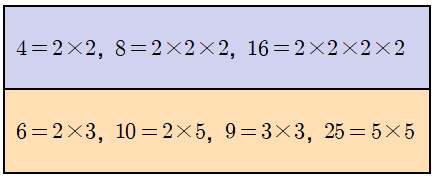
이와 같은 이유로 소수(素數)(prime number)는

자연수의 바탕이 되는 수라는 뜻을 가지고 있다.

 

tip) 소수(小數)(decimal) 0보다 크고 1보다 작은 소수

 

 

수많은 자연수 중에서 소수를 쉽게 찾는 방법은 없을까 하고 

고민한 그리스의 수학자 에라토스테네스의 방법을 알아보자.

[출처 네이버 지식백과]

1은 소수가 아니므로 지운다.

2는 남기고 2의 배수를 모두 지운다.

3은 남기고 3의 배수를 모두 지운다.

4는 2의 배수이므로 지워졌으니 패스한다.

5는 남기고 5의 배수를 모두 지운다.

이와 같은 방법으로 남은 수 중 처음 수는 남기고

그 수의 배수를 모두 지운다.

 

소수의 배수는 자기 자신을 제외하면 모두 합성수이다.

이 원리를 이용하면 1부터 50까지의 자연수 중에서 

소수를 쉽게 찾을수 있다.

 

이때 지워지지 않고 남은 수가 모두 소수이다.

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47

 

수학종결자는 모든개념을 백지위에 쓸수 있다.